In order to understand why KB = 1024 Bytes (or is it?) you’ll need some prerequisites. To keep this blog beginner friendly I’ll be explaining some basics concepts such as: Positional Number Systems, SI Prefixes. If you already have a grasp of those concepts you can scroll past them to “Putting it all together” section or if you’re unfamiliar with the concepts or simply want to get a refresher you can opt to read the entire article :).
Positional Number System & Base 10, 2:
So when you say one-thousand-four-hunderd-and-three the number “1403” comes to mind. Why don’t we read it as one-four-zero-three? This is where the positional number system come in where the position of the number represents its value. Let’s explore this even more:
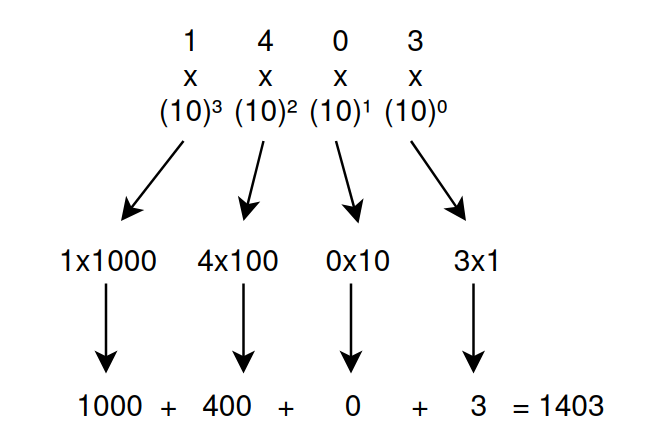
Hopefully the image explain the concept clearly. Another question that might arise is: Why are we raising 10 to powers and not some other number? Well it because we’re currently using base 10 decimal system numbers (0-9) in total 10 numbers.
So now onto Base 2:
Like Base 10 Base 2 is also positional number system and it works as following:
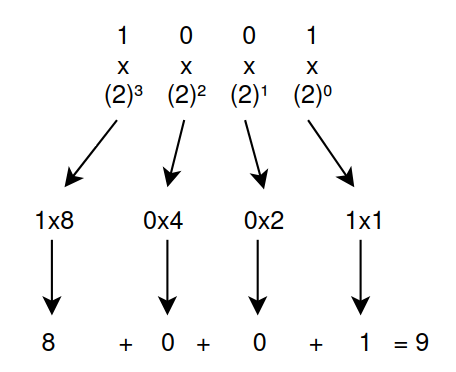
As before we have some numbers, but the difference is we only have 2 symbols at our disposal 1 and 0 instead of 0-9 (That’s Binary!). Using the same principles as before raising 2 to powers this time we can translate binary into a base 10 integer as shown in the image.
Si Prefixes:
We have heard the term Kilogram which represents 1000 grams. We know this because of the “Kilo” Prefix before the gram this is a part of the SI prefixes which are used to represent quantities of something. Here is the SI table of prefixes used to represent different quantities of something:
| Name | Symbol | Factor | Amount |
| giga | G | 109 | billion |
| mega | M | 106 | million |
| kilo | k | 103 | thousand |
| hecto | h | 102 | hundred |
| deka | da | 101 | ten |
Following this table let’s try convert a gram into a Kilogram.
Let:
Gram = 1
= 1 x 103
= 1 x 1000
= 1000 grams or 1 Kilogram
Putting it all together:
So now that we have an idea of how Binary works and how SI prefixes works let’s see how they fit in here. Initially when computer scientists wanted to define 1 KB they refereed to the 210 (1024) bytes instead of 103 (1000) bytes why did they do that? Well the reason become much clear when you look at this chart of 20-10

Since they didn’t have an exact name for 210 (1024) they went for the prefix Kilo and that’s where the problems occur.
Moving on:
In 1999 the IEC (International Electrotechnical Commission) introduced a new unit prefix system to resolve the issue called Binary Prefixes which are essentially SI Prefixes but adjusted with Binary so a KiloBinary(Kibi) = 1024 bytes and MegaBinary(Mebi) = 1024 Kibi and so on. Here’s a comparison between Binary and SI prefixes
However this system of prefix has not been widely adopted up until now, but in technicality now 1 KB strictly equals to 1000 Bytes and 1 KibiByte equals to 1024 Bytes. And computers still use the old prefix convention.
This is also why storage device manufacturing companies can get away with advertising a hard drive as 1 TB while having the (Gibi) 931 GB of storage. As they can argue that 1 TB = 1012 Bytes (1000000000000) instead of 1 TB = 240 (1099511627776) Bytes which is 931 Gebi(Or computers’ GB), essentially misleading people to believe they’re getting 1 TebiByte.
Finally now equipped with this knowledge whenever you hear your friend say this image’s size is 3.4 MB you can quickly correct them by saying it’s actually 3.4 Mebi to save them from the embarrassment.